Chain Replication
Examining Alternate Structures in Chain Replication
The paper “Chain Replication for Supporting High Throughput and Availability” by Robbert Van Renesse and Fred B. Schneider describes an algorithm for replication that can guarantee strong consistency while not sacrificing throughput or availability. The authors contend in the first few pages of their paper that system implementors will often sacrifice consistency in lieu of availability or throughput, but that this isn’t necessary with chain replication.
The consistency is guaranteed by chaining together nodes and by accepting updates at the head of the chain and queries at the tail. It is assumed that replies are sent for both updates and queries and these are sent from the tail. This results in the following structure:
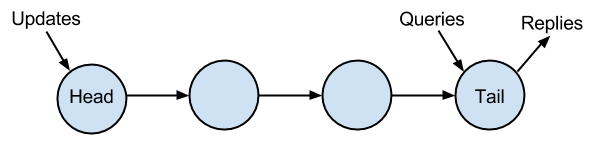
You can see that this does not inhibit throughput since the updates can be accepted at the head and pushed down the chain toward the tail, in a FIFO manner. Since the client requesting the update is waiting for a reply, it is guaranteed that every query post-update will be consistent. Also, queries can be accepted rapidly and pushed down the chain in order, so from an asynchronous viewpoint, updates are performed in order.
What stood out to me is the potential latency in this system. I understand that the single chain model lends itself to easy logical proof, but sending the updates through every node in the cluster seems that it would result in high performance cost. Each update is required to travel over N-1 paths prior to the reply being sent. The total latency being the sum of latency on each of the paths.
Could I think of a better structure that would reduce the latency between the updates and the update-reply while maintaining that the entire structure of nodes received the updates in order?
A parallel chaining method seems like it would be superior in terms of latency, but might require the Tail node to have more logic.
I came up with this, after some white-boarding:
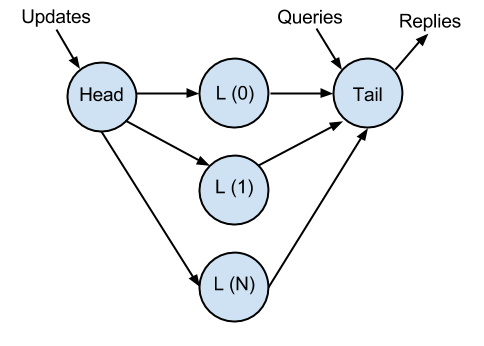
In the above structure, we have three elements – Head, Link(1 .. N), Tail. The chain works as a three-node chain would work with the described chain replication in the paper, with a few modifications:
- The Tail node maintains a count of replies per-update. It does not reply to an update until it receives N copies of the update from all Link nodes.
- Updates are processed FIFO in order received from L(0) - this eliminates path speed difference causing updates from arriving out of order on multiple paths.
This gives us a few benefits not available to us in the traditional single-link chain model:
- Latency is reduced from the sum of latency on all paths to the max latency of the slowest path.
- This gives us built-in failure detection, which was assumed in the chain replication paper. If fewer than N copies of an update are received at the tail, we can suspect that node of failure. We can implement a node failure procedure without reordering the chain in the event that the failure is on nodes L1…N.
- In the event of a failure of L(0), any of the other nodes are promoted to L(0) and last updates are re-transmitted from Head.
Both the original chain replication described in the paper and the above structure I described meet the description in the paper of the primary/backup approach. Both approaches ensure strong consistency by implementing a method to sequence requests through the structure. Both approaches distribute the updates to other servers. Both approaches send an update reply only after they have received acks from all non-failed servers in the structure.
However, an important distinction is that the authors have assumed that a primary/backup system consists only of a single primary server that is responsible for all updates, queries, and replies. The method I describe does not follow this model, but is rather a hybrid parallel chain model.
The authors of the paper provided data from a series of experiments they performed to compare varying types of chain replication. The interesting thing about their experiments is that they assumed a fixed latency per path, where in real world implementations, this will vary. Also, as I stated earlier, they assume that all client communication is done by a single primary in their primary/backup simulations.
The simulations show that chain replication has equal or superior performance in their tests to primary/backup when there is a single node responsible for all client communication. However the authors state that they think this is due to the bottleneck of the single server replier.
In conclusion, this paper presents a replication protocol that is very proof-friendly and that guarantees consistency, but I think that we can improve upon the suggested algorithm by evaluating different parallel structures. These structures can possibly eliminate costly chain reorganization procedures in many cases and reduce overhead in the event of failure. I think this is an area of research that would be interesting to continue investigating.